Errata #3

Brian spotted an arithmetic error in the Weight Update Worked Example section.

One of the weights should have been 3.0 not 4.0, which then affects the rest of the calculations.

Here is the corrected section below. The corrected error is highlighted, and this then flows onto the rest of the calculations.

The books will be updated, and you can ask Amazon for a free ebook update if you have that version.

---

Weight Update Worked Example

 

Let’s work through a couple of examples with numbers, just to see this weight update method working. 

The following network is the one we worked with before, but this time we’ve added example output values from the first hidden node o j=1 and the second hidden node o j=2 . These are just made up numbers to illustrate the method and aren’t worked out properly by feeding forward signals from the input layer.

We want to update the weight w 11 between the hidden and output layers, which currently has the value 2.0.
Let’s write out the error slope again. 

Let’s do this bit by bit:

• ●  The first bit ( t k ­ o k ) is the error e 1 = 1.5, just as we saw before.
  
• ●  The sum inside the sigmoid functions Σ j w jko j is (2.0 * 0.4) + (3.0 * 0.5) = 2.3.
  
• ●  The sigmoid 1/(1 + e­ 2.3 ) is then 0.909. That middle expression is then 0.909 * (1 ­ 0.909) = 0.083.
  
• ●  The last part is simply o j which is oj =1 because we’re interested in the weight w 11 where j = 1. Here it is simply 0.4. 

Multiplying all these three bits together and not forgetting the minus sign at the start gives us ­0.04969. 

If we have a learning rate of 0.1 that give is a change of ­ (0.1 * ­ 0.04969) = + 0.005. So the new w 11 is the original 2.0 plus 0.005 = 2.005. 

This is quite a small change, but over many hundreds or thousands of iterations the weights will eventually settle down to a configuration so that the well trained neural network produces outputs that reflect the training examples.

Error Backpropagation Revisted

A great question from Alex J has prompted a deeper look at how we take the error at the output layer of a neural network and propagate it back into the network.

Reminder: Error Informs Weight Updates

Here's a reminder why we care about the error:

• In a neural network, it is the link weights that do the learning. They are adjusted again and again in an attempt to better match the training data.
• This refinement of the weights is informed by the error associated with a node in the network. A small error means we don't need to change the weights much. 
• The error at the output layer is easy - it's simply the difference between the desired target and actual output of the network.
• However the error associated with internal hidden layer nodes is not obvious.

What's The Error Inside The Network?

There isn't a mathematically perfect answer to this question.

So we use approaches that make sense intuitively, even if there isn't a mathematically pure and precise derivation for them. These kinds of approaches are called heuristics.

These "rule of thumb" heuristics are fine ... as long as they actually help the network learn!

The following illustrates what we're trying to achieve - use the error at the output layer to work out, somehow, the error inside the network.

Previously, and in the book, we considered three ideas. An extra one is added here:

• split the error equally amongst the connected nodes, recombine at the hidden node
• split the error in proportion to the link weights, recombine at the hidden node
• simply multiply the error by the link weights, recombine at the hidden node
• the same as above but attempt to normalise by dividing by the number of hidden nodes

Let's look at these in turn, before we try them to see what performance each approach gives us.

1. Split Error Equally Amongst Links

We split the error at each output node, dividing it equally amongst the number of connected incoming links. We then recombine these pieces at each hidden layer node to arrive at an internal error.

Mathematically, and in matrix form, this looks like the following. $N$ is the number of links from hidden layer nodes into an output node - that is, the number of hidden layer nodes.

$$
e_{hidden} =
\begin{pmatrix}
1/N & 1/N & \cdots \\
1/N & 1/N & \cdots  \\
\vdots & \vdots & \ddots \\
\end{pmatrix}
\cdot e_{output}
$$

Remember that a matrix form is really useful because Python's numpy can do the calculations efficiently (quickly) and we can write very concise code.

2. Split Error In Proportion To Link Weights

We split the error, not equally, but in proportion to the link weights. The reason for this is that those links with larger weights contributed more to the error at the output layer. That makes intuitive sense - small weights contribute smaller signals to the final output layer, and should be blamed less for the overall error. These proportional bits are recombined again at the hidden layer nodes.

Again, in matrix form, this looks like the following.

$$
e_{hidden} =
\begin{pmatrix}
\frac{w_{11}}{w_{11} + w_{21} + \cdots} & \frac{w_{12}}{w_{12} + w_{22} + \cdots} & \cdots \\
\frac{w_{21}}{w_{11} + w_{21} + \cdots} & \frac{w_{22}}{w_{12} + w_{22} + \cdots} & \cdots \\
\vdots & \vdots & \ddots \\
\end{pmatrix}
\cdot e_{output}
$$

The problem is ... we can't easily write this as a simple combination of matrices we already have, like the weight matrix and the output error matrix. To code this, we'd lose the benefits of numpy being able to accelerate the calculations. Even so, let's try it to see how well it performs.

3. Error Simply Multiplied By Link Weights

We don't split the error, but simply multiply the error by the link weights. This is much simpler than the previous idea but retains the key intuition that larger weights contribute more to the networks error at the output layer.

You can see from the expression above that the output errors are multiple day the weights, and there is also a kind of normalisation division. Here we don't have that normalisation.

In matrix form this looks like the following - it is very simple!

$$
e_{hidden} = w^{T} \cdot e_{output}
$$

Let's try it - and if it works, we have a much simpler heuristic, and one that can be accelerated by numpy's ability to do matrix multiplications efficiently.

4. Same as Above But "Normalised"

This additional heuristic is the same as the previous very simple one - but with an attempt to apply some kind of normalisation. We want to see if the lack of a normalisation in the simple heuristic has a negative effect on performance. 

The expression is still simple, the above expression divided by the number of hidden nodes $N$.

$$
e_{hidden} = \frac{w^{T}}{N} \cdot e_{output}
$$

You can imagine this goes some way to allaying fears that the previous approach magnifies the error unduly. This fear goes away if you realise the weights can be $<1$ and so can have a shrinking effect, not just a growing effect.

Results!

The above heuristics were coded and compared using the MNIST challenge. We keep the number of hidden nodes at 100, and the learning rate at 0.1 We do vary he number of learning epochs over 1, 2 and 5.

The following shows the results.

We can make some interesting conclusions from these results.

Conclusions

• Naively splitting the error equally among links doesn't work. At all! The performance of 0.1 or 10% accuracy is what you'd get randomly choosing an answer from a possible 10 answers (the digits 0-9).
• There is no real difference between the sophisticated error splitting and the much simpler multiplication by the link weights. This is important - it means we can safely use the much simpler method and benefit from accelerated matrix multiplication.
• Trying to normalise the simple method actually reduces performance ... by slowing down the learning rate. You can see it recover as you increase the number of learning epochs.

All this explains why we, and others, choose the simpler heuristic. It's simple, it works really well, and it can benefit from technology that accelerates matrix multiplication ... software like Python's numpy, and hardware like GPUs through openCL and CUDA.

---

I'll update the book so readers can benefit from a better explanation of the choice of heuristic. All ebooks can be updated for free by asking Amazon Kindle support.

Bias Nodes in Neural Networks

I've been asked about bias nodes in neural networks. What are they? Why are they useful?

Back to Basics

Before we dive into bias nodes .. let's go back to basics. Each node in a neural network applies a threshold function to the input. The output helps us make a decision about the inputs.

We know the nodes in a real neural network are usually sigmoid in shape, with the $1/(1+e^{-x})$ logistic function and the $tanh()$ function also being popular.

But before we arrived at those, we used a very simple linear function to understand how it could be used to classify or predict, and how it could be refined  by adjusting its slope. So let's stick with linear functions for now - because they are simpler.

The following is a simple linear function.

$$y = A\cdot x$$

You'll remember it was the parameter $A$ that we varied to get different classifications. And it was this parameter $A$ that we refined by learning from the error from each training example.

The following diagram shows some examples of different lines possible with such a linear function.

You can see how some lines are better at separating the two clusters. In this case the line $y=2x$ is the best at separating the two clusters.

That's all cool and happy - and stuff we've already covered before.

A Limitation

Look at the following digram and see which line of the form $y=A\cdot x$ would best separate the data.

Ouch! We can't seem to find a line that does the job - no matter what slope we choose.

This is a limitation we've hit. Any line of the form $y= A\cdot x$ must go through the origin. You can see in the diagram all three example lines do.

More Freedom

What we need is to be able to shift the line up and down. We need an extra degree of freedom.

The following diagram shows some example separator lines which have been liberated from the need to go through the origin.

You can see one that does actually do a good job of separating the two data clusters.

So what form do these liberated lines take? They take the following form:

$$ y = A \cdot x + B $$

We've added an extra $+B$ to the previous simpler equation $y = A\cdot x$. All this will be familiar to you if you've done maths at school.

Bias Node

So we've just found that for some problems, a simple linear classifier of the form $y=A\cdot x$ was insufficient to represent the training data. We needed an extra degree of freedom so the lines were freer to go all over the data. The full form of a linear function $y = A\cdot x + B$ does that.

The same idea applies even when we're using sigmoid shaped functions in each neural network node. You can see that without a $+B$ those simpler functions are doomed to stick to a fixed origin point, and only their slope changes.  You can see this in the following diagram.

How do we represent this in a neural network?

We could change the activation function in each node. But remember, we chose not to alter the slope of that function, never mind adding a constant. We instead chose to change the weights of the incoming signals.

So we need to continue that approach. The way to do this is to add a special additional node into a layer, alongside the others, which always has a constant value usually set to 1. The weight of the link is able to change, and even become negative. This has the same effect of adding the additional degree of freedom that we needed above.

The following illustrates the idea:

The activation function is a sigmoid is of the combined incoming signals $w_0 + w_1\cdot x$. The $w_0$ is provided by the additional node and has the effect of shifting the function left or right along the x-axis. That in effect allows the function to escape being pinned to the "origin" which is $(0, \frac{1}{2})$ for the logistic function and $(0,0)$ for the $tanh()$.

Don't forget that the $w_1$ can be negative too ... which allows the function to flip top to bottom too, allowing for lines which fall not just rise.

The following shows how the extra node is included in a layer. That node is called a bias node.

It is worth experimenting to determine whether you need a bias node to augment the input layer, or whether you also need one to augment the internal hidden layers. Clearly you don't have one on the output layer.

Coding A Bias Node

A bias node is simple to code. The following shows how we might add a bias node to the input layer, with code based on our examples in github.

• Make sure the weight matrix has the right shape by incrementing the number of input nodes, self.inodes = input_nodes + 1.

• This automatically means that the weight matrix takes the right shape, self.wih depends on self.inodes.

• In the query() and train() functions, the inputs_list has a 1.0 bias constant input prepended or appended to it.

Why Didn't We Use Bias?

Why didn't we use bias when we created a neural network to learn the MNIST data set?

The primary aim of the book was to keep things as simple as possible and avoid additional details or optimisations as much as possible.

The MNIST data challenge is one that happens not to need a bias node. Just like some cluster separation problems don't need the extra degree of freedom.

Simple!

Talk from PyData London 2016

Here's my talk 'A Gentle Intro To Neutral Networks (with Python)' from Pydata London 2016.

It was a great event, meeting old friends, making new ones, and learning lots too ... all with a  great grass-roots community vibe.

Here's the youtube PyData channel for the rest of the talks .. a real treasure trove!

Complex Valued Neural Networks - Experiments

Update: the link between the phase rotated by these neurons and frequency components of an image is not clear. Needs more work ...

---

There are many ways to change the popular model of neural networks to see if we can improve how they work.

For example, we could change the activation function, or how nodes are connected to each other, or try different error functions. These things are being done fairly often and aren't considered that radical.

The following talks about a much deeper, more fundamental change.

1. From Real Numbers to Complex Numbers

Complex numbers are a richer set of numbers than the normal real numbers that we predominantly use in neural networks.

They have a higher dimensionality which should allow much more complicated relationships to be learned by a neural network.

We know that often have to recast a problem into a higher dimensional space in order for a learning method to work - such as projecting 1-dimensional XOR data into a higher dimensional space so that a linear, but higher-dimensional, threshold can partition the data.

Is it enough to simply replace the use of real values with complex values, and keep everything else the same - the same activation function, the same error function, the same system of link weights, etc? Hmmmm ...

2. Complex Valued Link Weights

The first idea of a thing to upgrade from normal real numbers to complex values is the link weights.

That itself is actually a massive change because now signals are not just amplified or diminished as they pass through a network, they can now be rotated too.

This is a significant step change in the richness of what a neural network can do to the signals - some call this higher functionality. It should lead to a richer ability to learn more complex relationships in training data.

Why rotation? Because multiplying by a complex number doesn't just change a value's magnitude, it can also change the direction ... a rotation. A simple example is multiplying by (0+1j) rotates a value anti-clockwise by 90-degrees ($\pi /2$ radians).

If we're now processing complex values, we need to think again about the nodes too. Do they need to change as well?

3. Complex Neural Nodes

Traditional neural network nodes do two things. They sum up the incoming signals, moderated by the link weights, and they then use an activation function to produce an output signal. That activation function has historically been S-shaped or step-shaped to reflect how we thought biological neurons worked.

We could keep that as it is. And some researchers have tried that - trying to use the logistic function $1/(1+e^{-x})$, or the $tanh()$ function, with complex inputs. Some problems arise from this, though. The calculations are not easy. The gradient isn't trivial to calculate to do gradient descent, if at all (not an expert but iirc you can't differentiate it wrt complex values). There isn't a great fit between rotating signals and an activation threshold function that assumed a simple incoming signal whose magnitude was the only thing of importance.

So let's be radical and try something very different.

Let's force the signal to have a magnitude of 1, but allow it to rotate. That means we are working with signals that only sit on the unit circle in the complex domain. In essence we've discarded the magnitude and kept the phase.

This may seem radical, but isn't really when you think about it. We hope the benefits of the complex domain are in the ability for signals to rotate around. Absolute magnitude was never that important anyway in traditional neural networks as we routinely normalised signals, and it was the relative magnitude at the output layer that was used for eventually deciding on a category or class. Remember the logistic and $tanh()$ activations squish the signal's magnitude into a specific range, irrespective of the incoming magnitude.

So what does a complex node's activation function do? It doesn't really need to do anything more that what we've just described. The incoming signals have already been rotated by the complex weights, so all that remains is to make sure the sum is rescaled back to a unit circle.

That's it!

Here's what we've just said, in mathematical notation:

1. Combine incoming signals to a node $$ z = \sum_{n}{w_n \cdot x_n} $$
2. Rescale back to the unit circle $$ P(z) = \frac{z}{|z|} = e^{j * arg(z)} $$

Preparing Inputs, Mapping Outputs

Ok so in our mind we've designed a machine which kinda has lots of cogs in it, rotating the signals as they pass through. And we've said that we're constraining these signals to a magnitude of 1, that is, they're always on a unit circle.

How does this work with inputs that might be from the real world, and not complex numbers on a unit circle? And what about the answers we want from a neural network? We might want a network to give us answers that are larger real numbers, or maybe even classification categories with names like "dog, cat, mouse".

From our work on traditional neural networks, we've already seen the need to prepare inputs, and also to map the outputs.

Inputs

Inputs need to map to the complex unit circle. Why? Imagine we had a super-simple network of only one node. That node takes the input and needs to map that to an answer. To do this, it needs to do something to that data, a transformation, the application of a function. To give the node the best chance of learning to do this, the incoming data should be as best spread out over that transformation's domain space as possible. We know that relatively low variance can hinder learning.

Input values that run only along the real axis (imaginary part is zero) have only 2 possible phases - 0 or $\pi$ radians. For a network, or indeed a node, that tries to work with phases in order to make a decision, this is extremely limiting. So we need to map the inputs to the unit circle and cover a good range of phases. How we do this depends on the specifics of a particular problem, but a good starting point is to linearly remap the minimum of the input values to $e^{j \cdot \theta=0}$, and the maximum to $e^{j \cdot \theta=2\pi}$.

In some scenarios the input values shouldn't wrap around. That is, if we had categories like the letters A to Z, then A is not semantically close to Z, but would be when mapped to the unit circle. We can insert a mapping gap - to ensure that a small change in A doesn't lead to Z. 

If we have categories, rather than a continuum of input values, then it makes sense to divide the unit circle into sectors. For example, insect body lengths are a continuum, and so can map to the unit circle fairly easily. Insect names, however are words, not continuous real numbers, so we need to take hard firm slices of the circle, as illustrated further down.

Outputs

In a similar way, we can map a node's output back to meaningful values, labels or classes.

If we had a continuum of real numbers, we can simply reverse the previous mapping back from the unit circle.

If we have nominal categories, we slice up the circle into sectors, as shown in the diagram below. You can also see why a sector's bisector should be the target value for training. Easy!

Aside: Phase is Important

Phase is incredibly important in signals from the real world. Let's illustrate how important.

Take an image of something from the real world, and decompose the signal into its frequency phase and magnitude. You might recognise this as taking a Fourier transform. If we reconstruct the image as follows:

• ignore the phase (set it all to 0), just use the magnitude
• ignore the magnitude (set it all to 1), just use the phase

we find the the phase contains most of the information we use to understand an image - not the magnitude.

Code to demonstrate this working is on github - it shows clearly that there is much more recognisable information in the phase part of an image's Fourier transform.

This exercise illustrates quite powerfully the importance of phase, and why a neural network based on processing and learning phase might be a good idea, particularly for image recognition tasks.

Learning Algorithm

We changed the activation function from an sigmoid shaped real function to a mapping of a signal to the unit circle. What does this mean for our learning algorithm?

The first thing to realise is that the mapping $P(z) = \frac{z}{|z|} = e^{1j*arg(z)}$ is not differentiable in the complex domain (doesn't satisfy the Cauchy-Riemann conditions). Remember, we needed to differentiate the activation function so we could do gradient descent down the error function to find better and better weights.

We don't need to do that here.

That's right. We don't need to differentiate. Or do gradient descent.

Have a look at the following digram which shows the actual output from a complex node and what the target output should be. Also illustrated is the correction that's needed - the error.

Lets write out what's happening to the signal in symbols. From above, we already have:

$$ z = \sum_{n}{w_n \cdot x_n} $$

$$ P(z) = \frac{z}{|z|} = e^{1j * arg(z)} $$

Now suppose we had the correct weight adjustments $\Delta w_n$ to make the $z$ point in the same direction as the desired training target $t$. Actually we can make it not just point in the same direction, we can imagine we've got the magnitude spot on too.

$$ t =  \sum_{n}{(w_n + \Delta w_n) \cdot x_n} $$

The error, which is the required correction, $e = t - z$, is

$$ e =  \sum_{n}{(w_n + \Delta w_n) \cdot x_n} - \sum_{n}{(w_n) \cdot x_n} $$

Simplifying,

$$ e = \sum_{n}{\Delta w_n \cdot x_n} $$

Ok - that's a nice simple relationship. It tells us the error $e$ is made up of many contributions from the various $\Delta w_n \cdot x_n$. But we don't have any more clues as to which values of $\Delta w_n$ precisely. Right now, it could be one of many different combinations ... just like $1+4=5$, $2+3=5$, $5+0=5$, and so on.

We could break this deadlock by assuming that each of the $\Delta w_n \cdot x_n$ contributes equally to the error $e$. That is for each of the N contributing nodes,  $\Delta w_n \cdot x_n = \frac{e}{N}$.

Is this too naughty?! It might be, but we've done similar cheeky things before with traditional neural networks, where the back propagation of the error is done by dividing it up heuristically, not by some sophisticated analysis.

We can now use this simpler expression and get $\Delta w_n$ on its own, which is what we want.

$$ \Delta w_n \cdot x_n = \frac{e}{N} $$

Normally we'd multiply both sides by $x^{-1}$. But remember, for complex numbers $x^{-1} = \frac{\bar{x}}{|x|}$. Remember also that the signals $x$ are on the unit circle so $|x|=1$, leaving $x^{-1}=\bar{x}$. That gives us,

$$ \Delta w_n = \frac{e}{N} \cdot \bar{x} $$

That's it! The learning rule ... no gradient descent, no differentiation ... just a simple error correction rule.

Let's try it!

Experiment 1: Boolean OR, AND

The code for a single neuron, and a small complex valued neural network, learning the Boolean relations OR and AND are on github.

So that's encouraging .. it works. We've shown the incredibly simple error correction learning method works - no need for derivatives and gradient descent.

But that test wasn't so challenging. Let's try a tougher test.

Periodic Activation Function

The complex valued neural node was easy to build and make, and experiments seem to confirm that it learns pretty quickly too.

But a simple node still has problems with the traditionally challenging problems like learning XOR. With a traditional neural network this needs multiple nodes to solve.

Aizenberg proposes that we can solve XOR with a single node, but to do that we need to make the activation function periodic. What does this mean? It means we enrich the process of mapping the unit circle to an output class. Instead of dividing the circle in sectors, one sector for each class, we have multiple sectors for each class. Each sector is then smaller. Also the sectors for the same class can't be next to each other - that would defeat the idea! A picture shows this best:

The learning process is the same as before, but this time we have a choice of target sectors for each actual output during training. Look at the diagram above - if the training target was "grass" which one of the two do we choose? Remember, the error depends on how far the actual output is from the training target, and here we seem to have two "grass" targets.

What do we do? We pick the nearest one.

Let's try it!

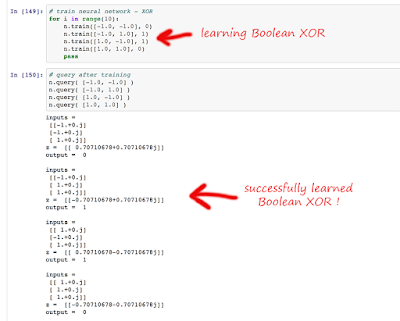
Experiment 2: Boolean XOR

The code for a single complex neuron with a periodic activation function is on github. We've used a periodicity of 2 for two classes (0, 1) .. which means a unit circle has four sectors corresponding to classes 0, 1, 0, 1.

It works! So we have a single complex node, learning XOR .. something that wasn't possible with traditional neural nodes.

Let's now try it on the famous Iris dataset, which is more of a challenge for most learning algorithms.

Experiment 3: Fisher's Iris Dataset

The Iris data set has a long history of challenging machine learning researchers. The data is simple enough - sepal and petal measurements of three species of Iris flower. The following scatterplot shows why it is a challenge - two of the three species have measurements which seem to intermingle into the same cluster.

Let's see how well a single complex neutron with a periodic activation function does.

The code is a github, and the following shows that with a periodicity of 3, we get 94.7% performance against a randomly partitioned test dataset (25% of the data set).

That is not bad at all! In fact, that's really rather impressive!

Microsoft's more complex example achieves 97% .. so we're not doing badly at all with very simple ideas and code .. and remember, only a single neuron!

Again ... to emphasise this ... an academic paper [PDF, table 2] shows similar scores of 95-97% using more complex networks.

How do we choose the right periodicity? I don't know. At this stage it is trial and error to choose the right periodicity.

Conclusion

We've achieved:

• a very simple approach to neural networks that reflects the importance of phase
• a super simple learning algorithm that avoids differentiation and gradient descent
• a powerful approach to learn non-threshold functions like XOR
• performance amongst the best from just a single complex neuron

Next time we'll see how these complex neurons can be combined into networks, and also see if we get good results from the MNIST handwriting challenge.

---

The ideas here are inspired by Igor Aizenberg, see more at his university course page.

Great Question from France: Training Order

I had a great question from Hamid from France, which led onto more interesting thoughts.

He assumed each training example was fed forward through the network many times, each time reducing the error, and wanted to know when to stop and move onto the next training example. That is:

Training Example 1: FW, BP, FW, BP,  FW, BP, ....
Training Example 2: FW, BP, FW, BP,  FW, BP, ....
Training Example 3: FW, BP, FW, BP,  FW, BP, ....
Training Example 4: FW, BP, FW, BP,  FW, BP, ....

( FW=Feed Forward, BP=Back Propagate )

---

My immediate reply was to say that this wasn't how it was normally done, but instead each training example was used in turn. Some call this on-line learning. That is:

Training Example 1: FW, BP
Training Example 2: FW, BP
Training Example 3: FW, BP
Training Example 4: FW, BP
...

And I said that it is often a good idea to repeat this several times, that is, training for several epochs.

---

Some will in fact batch together a few training examples and sum up the error to be used for back propagation. That is:

Training Example 1: FW (accumulate error)
Training Example 2: FW (accumulate error)
Training Example 3: FW (accumulate error)
Training Example 4: FW, BP accumulated error
Training Example 5: FW (accumulate error)
Training Example 6: FW (accumulate error)
Training Example 7: FW (accumulate error)
Training Example 8: FW, BP accumulated error

---

Then I thought about it more and concluded that Hamid's approach wasn't wrong at all - just different. He was asking what the stopping criteria would be for applying the same training data example many times. The real answer is .. I don't know - but I would experiment to find out.

---

Hamid's question is a good one, because it is not often made very clear which order or scheme is used. It is too easy for authors and teachers to assume new readers will know which scheme is being considered, or even which ones are a good idea.

That's why I love feedback from readers - they ask the best questions!

Thanks Hamid!

Slides for PyData London and EuroPython Bilbao 2016

I've been lucky enough to be chosen to talk at PyData London and EuroPython Bilbao 2016.

These are the slides - they're still in development and could change at anytime - but I thought I'd share in case someone found them useful.

https://goo.gl/JKsb62

I'll also be running a gentle intro session at the London Python Meetup Group in May too.

Republished as Kindle Textbook

After much deep thought I pulled my ebooks and republished them as Kindle Textbooks.

Why?

Well - the ebook format(s) are a pain.

• They're not sufficiently standardised for all parties to agree on.
• The quality of tools to create them is rubbish.
• And interoperability is a pain.

It's like web in the early days, different interests trying to subvert html, trying to "embrace, extent, extinguish". It took almost 20 years for the web to settle down around well understood common and open interoperable standards.

The epub format is open but still in flux. Amazon doesn't actually support it properly or directly - with lack of support in places, inconsistent support elsewhere, and additional proprietary features too. They have their own mobi, kf8 and azw formats too. And now kpf too. Their preview tools all work differently too - showing different results.

This is depressing - especially as it should be possible for all Kindles, old and new, to show text, follow basic links, and show images. Except they can't. Some do, some don't.

I felt bad about some users not being able to read the book properly .. so I had to act.

The new Kindle Textbook Creator works more like PDF - a format that preserves layout but at the cost of not being able to reflow text.

I made the decision that it was more important for the book to always work for readers - even if that meant fewer readers could buy the digital book. Older Kindles can't buy the book now it is in the new format. I am sad about that.

One day, digital book publishing will be fixed, or as fixed, as the web is today.

Error #2

Jon S pointed out that Deep Blue beat Gary Kasparov in 1997, not 1997 as stated in the introduction.

This will be fixed in the next updated content.

Error #1

Michael B found an error on page 32 of the book. That's the section where the idea of moderating the learning is introduced - a learning rate. The second training example uses a target value of 0.9. That's wrong, it should have said 1.9. The calculations which then update the slope A are wrong.

Below is the updated section, and the diagram has also been updated too.

---

Let’s press on to the second training data example at x = 1.0. Using A = 0.3083 we have y = 0.3083 * 1.0 = 0.3083. The desired value was 2.9 so the error is (2.9 - 0.3083) = 2.5917.  The ΔA = L (E / x) = 0.5 * 2.5917 / 1.0 = 1.2958. The even newer A is now 0.3083 + 1.2958 = 1.6042.

Let’s visualise again the initial, improved and final line to see if moderating updates leads to a better dividing line between ladybird and caterpillar regions.

This is really good!

Even with these two simple training examples, and a relatively simple update method using a moderating learning rate, we have very rapidly arrived at a good dividing line y = Ax where A is 1.6042.

---

The ebook has been updated and you should get an automatic update, or ask Amazon to trigger an update if it is slow to get to you. The print book has also been updated.

Busting Past 98% Accuracy

I was working on a document and expected to take a few hours ... so I thought, why not try a longer neural network training session to see if I could break past 98% performance.


The neural network architecture and training was boosted to:

• 300 hidden layer nodes
• 30 training epochs
• rotate training images +/- 10 degrees.

That took about 3 hours on my laptop!

The resultant performance did indeed break the previous record .. at 98.03%

 

The Book is Out!

Finally, the book is out!

Make Your Own Neural Network - a gentle introduction to the mathematics of neural networks, and making your own with Python.

You can get it on Amazon Kindle, and a paper print version is also be available.

IPython Neural Networks on a Raspberry Pi Zero

There is an updated version of this guide at http://makeyourownneuralnetwork.blogspot.co.uk/2017/01/neural-networks-on-raspberry-pi-zero.html

---

In this post we will aim to get IPython set up on a Raspberry Pi.

There are several reasons for doing this:

• Raspberry Pis are fairly cheap and accessible to many more people than expensive laptops.

• Raspberry Pis are very open - they run the free and open source Linux operating system, together with lots of free and open source software, including Python. Open source is important because it is important to understand how things work, to be able to share your work and enable others to build on your work. Education should be about learning how things work, and making your own, and not be about learning to buy closed proprietary software.

• For these and other reasons, they are wildly popular in schools and at home for children who are learning about computing, whether it is software or building hardware projects.

• Raspberry Pis are not as powerful as expensive computers and laptops. So it is an interesting and worthy challenge to be prove that you can still implement a neural network with Python on a Raspberry Pi.

I will use a Raspberry Pi Zero because it is even cheaper and smaller than the normal Raspberry Pis, and the challenge to get a neural network running is even more worthy! It costs about £4 UK pounds, or $5 US dollars. That wasn’t a typo!

Here’s mine.

Installing IPython

We’ll assume you have a Raspberry Pi powered up and a keyboard, mouse, display and access to the internet working.

There are several options for an operating system, but we’ll stick with the most popular which is the officially supported Raspian, a version of the popular Debian Linux distribution designed to work well with Raspberry Pis. Your Raspberry Pi probably came with it already installed. If not install it using the instructions at that link. You can even buy an SD card with it already installed, if you’re not confident about installing operating systems.

This is the desktop you should see when you start up your Raspberry Pi.

You can see the menu button clearly at the top left, and some shortcuts along the top too.

We’re going to install IPython so we can work with the more friendly notebooks through a web browser, and not have to worry about source code files and command lines.

To get IPython we do need to work with the command line, but it’ll be just once, and the recipe is really simple and easy.

Open the Terminal application, which is the icon shortcut at the top which looks like a black monitor. If you hover over it, it’ll tell you it is the Terminal. When you run it, you’ll be presented with a black box, into which you type commands, looking like the this.

Your Raspberry Pi is very good because it won’t allow normal users to issue commands that make deep changes. You have to assume special privileges. Type the following into the terminal:

sudo su -

You should see the prompt end in with a ‘#’ hash character. It was previously a ‘$’ dollar sign. That shows you now have special privileges and you should be a little careful what you type.

The following commands refreshes your Raspberry’s list of current software, and then updates the ones you’ve got installed, pulling in any new software if it’s needed.

apt-get upgrade

apt-get update

Unless you did this recently, there will likely be software that needs to be updated. You’ll see quite a lot of text fly by. You can safely ignore it. You may be prompted to confirm the update by pressing “y”.

Now that our Raspberry is all fresh and up to date, issue the command to get IPython. Note that, at the time of writing, the Raspian software packages don’t contain a sufficiently recent version of IPython to work with the notebooks we created earlier and put on github for anyone to view and download. If they did, we would simply issue a simple “apt-get install ipython3 ipython3-notebook” or something like that.

If you don’t want to run those notebooks from github, you can happily use the slightly older IPython and notebook versions that come from Raspberry Pi’s software repository.

If we do want to run more recent IPython and notebook software, we need to use some “pip” commands in additional to the “apt-get” to get more recent software from the Python Package Index. The difference is that the software is managed by Python (pip), not by your operating system’s software manager (apt). The following commands should get everything you need.

apt-get install python3-matplotlib

apt-get install python3-scipy

pip3 install ipython

pip3 install jupyter

pip3 install matplotlib

pip3 install scipy

After a bit  of text flying by, the job will be done. The speed will depend on your particular Raspberry Pi model, and your internet connection. The following shows my screen when I did this.

The Raspberry Pi normally uses an memory card, called an SD card, just like the ones you might use in your digital camera. They don’t have as much space as a normal computer. Issue the following command to clean up the software packages that were downloaded in order to update your Raspberry Pi.

apt-get clean

That’s it, job done. Restart your Raspberry Pi in case there was a particularly deep change such as a change to the very core of your Raspberry Pi, like a kernel update. You can restart your Raspberry Pi by selecting the “Shutdown …” option from the main menu at the top left, and then choosing “Reboot”, as shown next.

After your Raspberry Pi has started up again, start IPython by issuing the following command from the Terminal:

jupyter notebook

This will automatically launch a web browser with the usual IPython main page, from where you can create new IPython notebooks. Jupyter is the new software for running notebooks. Previously you would have used the “ipython3 notebook” command, which will continue to work for a transition period. The following shows the main IPython starting page.

That’s great! So we’ve got IPython up and running on a Raspberry Pi.

You could proceed as normal and create your own IPython notebooks, but we’ll demonstrate that the code we developed in this guide does run. We’ll get the notebooks and also the MNIST dataset of handwritten numbers from github. In a new browser tab go to the link:

• https://github.com/makeyourownneuralnetwork/makeyourownneuralnetwork

You’ll see the github project page, as shown next. Get the files by clicking “Download ZIP” at the top right.

The browser will tell you when the download has finished. Open up a new Terminal and issue the following command to unpack the files, and then delete the zip package to clear space.

unzip Downloads/makeyourownneuralnetwork-master.zip

rm -f Downloads/makeyourownneuralnetwork-master.zip

The files will be unpacked into a directory called makeyourownneuralnetwork-master. Feel free to rename it to a shorter name if you like, but it isn’t necessary.

The github site only contains the smaller versions of the MNIST data, because the site won’t allow very large files to be hosted there. To get the full set, issue the following commands in that same terminal to navigate to the mnis_dataset directory and then get the full training and test datasets in CSV format.

cd makeyourownneuralnetwork-master/mnist_dataset

wget -c http://pjreddie.com/media/files/mnist_train.csv

wget -c http://pjreddie.com/media/files/mnist_test.csv

The downloading may take some time depending on your internet connection, and the specific model of your Raspberry Pi.

You’ve now got all the IPython notebooks and MNIST data you need. Close the terminal, but not the other one that launched IPython.

Go back to the web browser with the IPython starting page, and you’ll now see the new folder makeyourownneuralnetwork-master showing on the list. Click on it to go inside. You should be able to open any of the notebooks just as you would on any other computer. The following shows the notebooks in that folder.

Making Sure Things Work

Before we train and test a neural network, let’s first check that the various bits, like reading files and displaying images, are working. Let’s open the notebook called “part3_mnist_data_set_with_rotations.ipynb” which does these tasks. You should see the notebook open and ready to run as follows.

From the “Cell” menu select “Run All” to run all the instructions in the notebook. After a while, and it will take longer than a laptop, you should get some images of rotated numbers.

That shows several things worked, including loading the data from a file, importing the python extension modules for working with arrays and images, and plotting graphics.

Let’s now “Close and Halt” that notebook from the File menu. You should close notebooks this way, rather than simply closing the browser tab.

Training And Testing A Neural Network

Now lets try training a neural network. Open the notebook called “part2_neural_network_mnist_data”. That’s  the version of our program that is fairly basic and doesn’t do anything fancy like rotating images. Because our Raspberry Pi is much slower than a typical laptop, we’ll turn down some of parameters to reduce the amount of calculations needed, so that we can be sure the code works without wasting hours and finding that it doesn’t.

I’ve reduced the number of hidden nodes to 50, and the number of epochs to 1. I still used the full MNIST training and test datasets, not the smaller subsets we created earlier. Set it running with “Run All” from the “Cell” menu. And then we wait ...

Normally this would take about one minute on my laptop, but this completed in about 25 minutes. That's not too slow at all, considering this Raspberry Pi Zero costs 400 times less than my laptop. I was expecting it to take all night.

Raspberry Pi Success!

We’ve just proven that even with a £4 or $5 Raspberry Pi, you can still work fully with IPython notebooks and create code to train and test neural networks - it just runs a little slower!